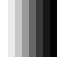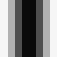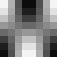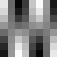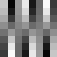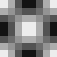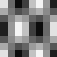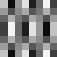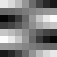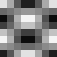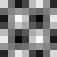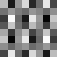4. DCT

Razlike u osjetljivosti ljudskog oka na podražaje različitih prostornih frekvencija od velikog su značaja za osmišljavanje sustava za kompresiju slike.

Slika se iz oblika kojim je predstavljena nekom transformacijom pretvara u niz valnih oblika različitih prostornih frekvencija. Dijelovi na koje je oko osjetljivo se ostavljaju, dok se ostali izostave.

Tri najznačajnija zahtjeva koja se postavljaju na metodu transformacije slike iz prostorne u frekvencijsku domenu su:

1. djelotvornost kompresije koja se očituje u mogućnosti metode da većinu energije koncentrira u nižim prostornim frekvencijama

2. jednostavnost računanja

3. minimalna srednja kvadratna pogreška

U teoriji se pokazalo da je najidealnija metoda za postizanje visokog stupnja kompresije Karhuneu-Loeve transformacija (KLT), no zbog velike zamršenosti postupka računanja pokazalo se da je nepraktična za primjenu.

Godine 1974. Ahmed, Natarajan i Rao su pokazali da DCT najbolje ispunjava gore navedene uvjete. Posjeduje gotovo identične karakteristike kao i KLT, ali i znatne prednosti. DCT ima, za razliku od KLT, nepromjenljiv algoritam računanja što je jako važno za aplikacije koje rade u stvarnom vremenu.

DCT je slična Fourier-ovoj transformaciji, no ona nije realni dio DFT. Slično kao i Fourier-ova transformacija DCT koristi kosinus funkcije nad diskretnim vrijednostima koje tretira kao diskretizirane 2-D valne oblike. U konkretnim primjenama (JPEG) zastupljenija je dvodimenzionalna DCT, no osnovni princip transformacije dan je sa jednodimenzionalnom DCT.

1-D DCT diskretnog niza f (x) i IDCT (inverzna DCT) diskretnog niza F(u) dane su sljedećim relacijama:

gdje je N duljina niza i C(u)= za u=0 i C(u)=1 za u > 0

ili u matričnoj formi , .

Općenito se primjenjuje 2-D verzija DCT nad M x N blokovima slike. Transformacija ulazne slike se dobiva u obliku M x N blokova DCT koeficijenata.

Transformacija i njoj inverzna dane su relacijama :

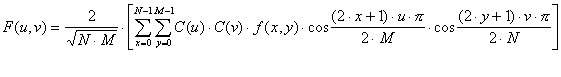
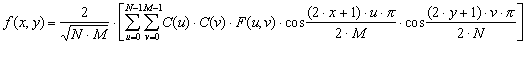
za u, v = 0

za u, v ¹ 0

Gore navedenim transformacijama DCT i IDCT omogućene su pretvorbe slike iz prostorne u frekvencijsku domenu i obratno.

Slika 4.1. Baza DCT

Element bloka slike određen je koordinatama x i y i opisan sa f(x,y), dok je njemu odgovarajući DCT koeficijent određen sa u i v i opisan sa F(u,v). DCT koeficijent predstavlja zastupljenost neke prostorne frekvencije u slici; rezultat je analiziranja cijelog bloka koji je vezan za srednju vrijednost slike (sumiranje). Za u=v=0 dobijemo istosmjerni ili DC koeficijent koji je vezan za srednju vrijednost slike, ostali koeficijenti se nazivaju AC koeficijenti. Ako DCT koeficijente prikažemo kao blok čiji elementi imaju indeks u, v, tada se idući s lijeva na desno povećava vodoravna komponenta prostorne frekvencije, a od gore prema dolje okomita komponenta. Maksimalna frekvencija je u donjem desnom kutu bloka. Na slici 4.1. prikazani su valni oblici za samo jedan AC koeficijent (položaj odgovarajućeg bloka u slici odgovara poziciji koeficijenta u DCT bloku. Blok koji ima vrijednost sredine između crnog i bijelog svih prikazanih realnih oblika je u gornjem lijevom kutu.

Uzmimo blok 8 x 8 čiji su elementi slučajni brojevi u intervalu [0,255]. Dodjelimo brojevima odgovarajuće razine sivog prema sljedećem pravilu : 0 je crno, 1-254 su svi tonovi sivog, a 255 je bijelo (slika 4.2. a) i b)).

198	208	19	209	60	156	241	151
157	16	215	212	124	67	175	119
165	243	182	162	197	252	156	182
192	80	221	38	202	193	228	218
36	0	222	199	194	122	2	46
152	193	193	186	60	240	76	117
229	78	170	143	161	91	246	230
43	182	229	184	58	20	25	4

a) b)

c) d)

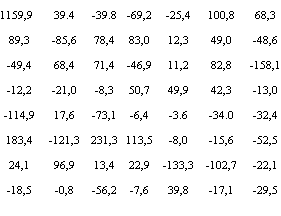
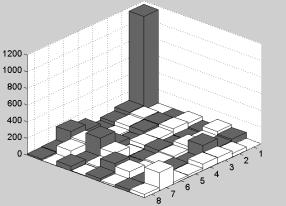
Slika 4.2. a), b) Vrijednosti uzoraka koji ulaze u transformaciju, c) vrijednosti dobivenih DCT koeficijenata, d) prikaz apsolutnih vrijednosti DCT koeficijenata

Nakon provedene DCT transformacije dobivamo blok DCT koeficijenata u 3-D koordinatnom Kartezijevom sustavu možemo prikazati apsolutne vrijednosti pojedinih AC koeficijenata (predstavljaju zastupljenost određene prostorne frekvencije).

Apsolutna vrijednost AC koeficijenata (odgovara visini u 3-D grafu) određena je koordinatama u, v koje određuju udaljenost od istosmjerne komponente.

Frekvencija u smjeru širenja osnovnog valnog oblika je gdje su w_x i w_y frekvencije u x i y smjeru određene sa udaljenosti odgovarajućeg AC i DC koeficijenta. Smjer s je smjer najvećih promjena valnog oblika. Ukoliko je potrebno prikazati zastupljenost određene prostorne frekvencije, bez obzira na smjer širenja, različite AC koeficijente sa jednakim w_s tretiramo jednako.

Frekvencijska analiza mirne slike (kakve nalazimo u prirodi) dana je na slici 4.3. Na apscisi je visina prostorne frekvencije (udaljenost od DC koeficijenata), a na ordinati je zastupljenost iste. Graf pokazuje pravilan pad zastupljenosti od nižih prema višim frekvencijama. Dakle, veći AC koeficijenti grupiraju se oko gornjeg lijevog kuta DCT bloka. To su koeficijenti koji predstavljaju valne objekte veće energije. Tu se nalaze podaci s visokom entropijom, tj. Koji nose veći dio informacije o slici. Pravilna distribucija koeficijenata s visokom entropijom omogućava njihovo izdvajanje od ostalih koeficijenata, te uspješnu kompresiju slike. Odbacivanjem viših prostornih frekvencija u slici vršimo niskopropusno filtriranje. Sada možemo procijeniti koeficijent kompresije kao omjer preostalih i početnih koeficijenata (na slici 4.6. su dani neki primjeri).

Slika 4.3. Frekvencijska analiza test slike Baboon

Da bi kompresija dala zadovoljavajuće rezultate potrebno je odabrati podatke o slici koji se mogu odbaciti bez da se vidno naruši kvaliteta slike. Kompresija će biti s gubicima, no smanjit će se broj potrebnih bitova što povlači manje prostora za pohranjivanje i brži prijenos informacije. Dobiveni blok DCT koeficijenata od ulaznog bloka se dijeli sa koeficijentima kvantizacije, te se tako dobiveni koeficijenti zaokružuju na cjelobrojne vrijednosti radi jednostavnijeg prikaza u binarnom obliku. Kvantizacijske tablice koje su istih dimenzija kao i DCT blokovi imaju manje koeficijente u gornjem lijevom kutu (odgovaraju nižim frekvencijama) od koeficijenata u preostalom dijelu bloka (više frekvencije). Veći kvantizacijski koeficijenti smanjuju ionako male DCT koeficijente nižih frekvencija te to znatno olakšava daljnje kodiranje. Nakon kvantizacije i zaokruživanja na cjelobrojnu vrijednost provodi se cik-cak raščlanjivanje AC koeficijenata. Posebno se odvaja DC koeficijent koji se DPCM postupkom kodira zajedno s ostalim koeficijentima. Primjenom cik-cak raščlanjivanja omogućena je pretvorba 2-D bloka u niz AC koeficijenata u kojem više frekvencije slijede jedna iza druge te to znatno olakšava njihovo kodiranje.

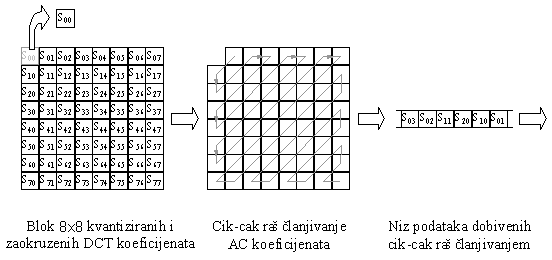
Slika 4.4. Cik-cak raščlanjivanje

Još jedan od važnih parametara svake metode kompresije je vrijeme izvođenja transformacije koje je obrnuto proporcionalno umnošku broja elemenata slike i broja elemenata bloka.

Slika 4.5. Ispitna slika baboon uz različite stupnjeve kompresije (desni stupac prikazuje razliku ulazne i rekonstruirane slike)

Povratak na sadržaj